Why Does MySQL Use B+ Trees Instead of Skip Lists for Indexing?

===============================================================

Today I saw a very useful and clear video about the explanation of B+ tree and skip lists in Database, so I want to write a blog to record my understanding.

When we think about MySQL tables, they seem to be simply storing rows of data, similar to a spreadsheet.

Directly traversing these rows of data gives us a performance of O(n), which is quite slow. To accelerate queries, B+ trees are used for indexing, optimizing the query performance to O(log n).

But this raises a question: there are many data structures with log(n) level query performance, such as skip lists used in Redis’s zset, which are also log(n) and even simpler to implement.

So why doesn’t MySQL use skip lists for indexing?

The Structure of B+ Trees

Generally, B+ trees are a multi-level structure composed of multiple pages, each being 16Kb. For primary key indexes, the leaf nodes at the lowest level hold row data, while the internal nodes hold index information (primary key id and page number) to speed up queries.

For instance, if we want to find row data with id=5, we start from the top-level page records. Each record contains a primary key id and a page number (page address). Follow the yellow arrow; to the left, the smallest id is 1, to the right, the smallest id is 7. Therefore, if the data with id=5 exists, it must be on the left side. Following the record’s page address, we arrive at page 6, then determine id=5>4, so it must be on the right side in page 105.

In page 105, although there are multiple rows of data, they are not traversed one by one. The page also has a page directory, which can speed up the query for row data through binary search, hence finding the row data with id=5 and completing the query.

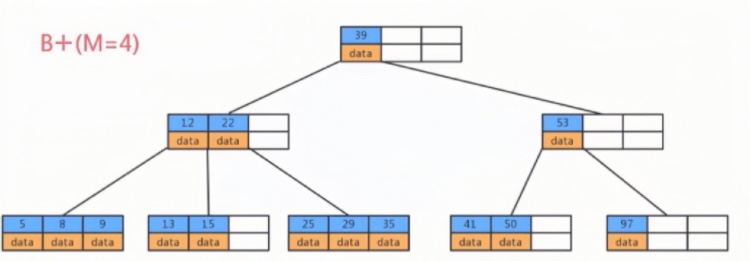
As we can see, B+ trees use a space-for-time approach (creating a batch of internal nodes to store index information), optimizing the query time complexity from O(n) to O(log n).

The Structure of Skip Lists

Having looked at B+ trees, let’s examine skip lists.

Similarly, they are used to store rows of data.

We can string them together in a linked list. To query a node in the list, the time complexity is O(n), which is too high. Thus, some linked list nodes are elevated to construct a new list. When I want to query data, I first check the upper list, which quickly tells me the range where the data falls, and then I jump to the next level for querying. This significantly narrows down the search scope.

For example, to query data with id=10, we first traverse the upper layer, sequentially assessing 1,6,12, and quickly determine that 10 is between 6 and 12. Then, jumping down a level, we can confirm the position of id=10 after traversing 6,7,8,9,10. The search range is effectively halved. If just two layers of linked lists can halve the search range, adding more layers would be even better, right?

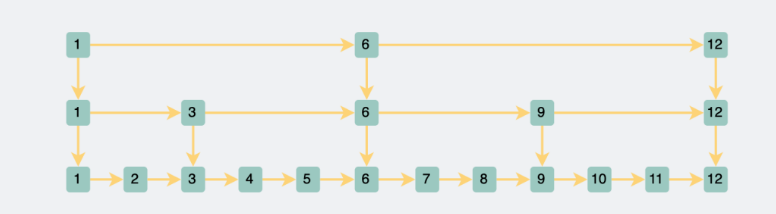
Thus, the skip list becomes multi-layered. To continue with our example of querying data with id=10, we would only need to search through 1,6,9,10 to find it, which is quicker than with two layers. It’s evident that skip lists also trade space for time to enhance query performance. The time complexity is log(n).

The Differences Between B+ Trees and Skip Lists

As we can see, the lowest level of both B+ trees and skip lists contains all the data, which is sequential and suitable for range queries. The upper levels are constructed to improve search performance. These two structures are strikingly similar. However, they differ in how they handle data insertion and deletion. Let’s discuss this with data insertion as an example.

B+ Tree Data Insertion

A B+ tree is essentially a multi-way balanced binary tree. The key lies in the word “balanced,” meaning for a multi-way tree structure, the heights of the subtrees are as consistent as possible (generally differing by no more than one level). This ensures that no matter which subtree branch you search, the number of searches won’t vary much.

As new data is continuously inserted into the database table, the B+ tree adjusts and splits data pages to maintain balance.

We know that a B+ tree is divided into leaf nodes and internal nodes.

When a piece of data is inserted, both the leaf node and its upper index node (internal node), which have a maximum capacity of 16k, may become full.

For simplicity, let’s assume a data page can only hold three rows of data or indexes.

There are three scenarios when inserting data, depending on whether the data page is full:

1. Neither the leaf node nor the index node is full. This is the simplest case; just insert directly into the leaf node.
2. The leaf node is full, but the index node is not. In this case, the leaf node must be split, and the index node must add new index information.
3. Both the leaf node and the index node are full. Both leaf and index nodes need to be split, and a new layer of indexing must be added above.

As we can see, only when both the leaf and index nodes are full does the B+ tree consider adding a new layer of nodes.

From previous articles, we know that it takes roughly 2 million entries to fill a three-layer B+ tree.

Skip List Data Insertion

A skip list is also multi-layered, and when new data is inserted, the lowest layer of the list needs to add the data.

At this point, is it necessary to add data for indexing in the upper layers?

This purely depends on a random function.

Theoretically, to achieve the effect of binary search, each layer’s node count should be half of the layer below it.

That is to say, now that new data has been inserted, there’s a 50% chance it will need to be indexed in the second layer, a 25% chance it will need to be indexed in the third layer, and so on up to the top layer.

For example, if data with id=6 is inserted and the random function returns the third layer (a 25% chance), then data must be inserted from the lowest to the third layer in the skip list. If this random function is designed as described, when there’s a sufficiently large sample size of data, the distribution will match our ideal “binary” distribution.

Unlike the B+ tree, whether a skip list adds layers depends purely on the random function and has nothing to do with neighboring nodes.

Why Does MySQL Use B+ Trees Instead of Skip Lists?

B+ trees are multi-way tree structures. Each node is a 16k data page that can hold a lot of index information, so the fan-out is very high. About three layers can store approximately 2 million entries (knowing the conclusion is enough, if you want to know the reason, you can refer to previous articles). That is, to query data, if those data pages are all on disk, then at most three disk IOs are needed.

A skip list is a linked list structure, with one node per piece of data. If the bottom layer needs to store 2 million entries and achieve binary search efficiency with each query, 2 million is roughly in the ballpark of 2 to the power of 24, meaning the skip list would be about 24 layers high. In the worst case, these 24 layers of data would be scattered across different data pages, or in other words, searching for data would entail 24 disk IOs.

Therefore, to store the same amount of data, the height of the B+ tree is less than that of the skip list. If placed in a MySQL database, this means fewer disk IOs and thus faster B+ tree queries.

As for write operations, B+ trees need to split and merge index data pages, whereas skip lists independently insert data and determine the number of layers based on a random function, without the cost of rotations and maintaining balance. Therefore, the write performance of skip lists is better than that of B+ trees.

In fact, MySQL’s storage engine can be changed. It used to be MyISAM, and then InnoDB came along, both using B+ trees for indexing. This means you could theoretically build a storage engine with skip list indexing for MySQL. In fact, Facebook created a RocksDB storage engine that uses skip lists. To put it simply, its write performance is indeed better than InnoDB’s, but its read performance is quite a bit worse.

Why Does Redis Use Skip Lists Instead of B+ Trees or Binary Trees?

Redis supports a variety of data structures, including a sorted set, also known as ZSET, which is internally implemented with skip lists. So why use skip lists instead of B+ trees or other structures?

This question almost always comes up in interviews.

Although I’m very familiar with it, every time I have to pretend I’ve never thought about it before and come up with the answer on the spot.

Really, it’s a test of acting skills.

As we know, Redis is a pure in-memory database.

Read and write operations are performed in memory and have nothing to do with the disk, so the height of the structure is no longer a disadvantage for skip lists.

Moreover, as mentioned earlier, B+ trees involve a series of merge and split operations. If we were to use a red-black tree or other AVL tree, there would be various rotations, all aimed at maintaining the balance of the tree.

However, when inserting data into a skip list, a simple random decision is made as to whether to add an index above, without any consideration for neighboring nodes and thus avoiding the cost of rotations and balancing.

Therefore, Redis chose skip lists over B+ trees.

Conclusion

B+ trees are multi-way balanced search trees with a high fan-out, requiring only about three layers to store approximately 2 million entries. Under similar conditions, skip lists would need about 24 layers. Assuming layer height corresponds to disk IO, B+ trees would have better read performance than skip lists, which is why MySQL chose B+ trees for indexing.

Redis operations are conducted entirely in memory, not involving disk IO. Skip lists are simple to implement, and compared to B+ trees, AVL trees, and others, they avoid the overhead of rotating tree structures, which is why Redis uses skip lists to implement ZSET instead of tree structures.

The storage engine RocksDB uses skip lists internally. Compared to InnoDB, which uses B+ trees, although it has better write performance, its read performance is indeed worse. In scenarios where reads are more frequent than writes, B+ trees are still considered superior.